Selesaian Sistem Persamaan Linear Tiga Variabel (SPLTV)

Dalam menyelesaikan sistem persamaan linear tiga variabel (SPLTV), ingat bahwa masing-masing persamaan memiliki grafik berupa suatu bidang datar dalam ruang tiga dimensi. Bidang-bidang tersebut dapat saling berpotongan dengan bermacam-macam cara, yang menghasilkan kemungkinan himpunan selesaian yang berbeda pula. Perhatikan ilustrasi berikut.

Sistem persamaan linear tiga variabel dapat memiliki tepat satu selesaian (a, b, c), jika bidang-bidang pada sistem tersebut berpotongan tepat di satu titik (gambar a). Dengan kata lain, titik ini memenuhi semua persamaan pada sistem tersebut. Apabila bidang-bidang tersebut berpotongan pada suatu garis (gambar b), maka sistem tersebut disebut tergantung secara linear (linearly dependent) dan terdapat selesaian yang tak hingga banyaknya. Tidak seperti kasus pada dua dimensi, persamaan garis pada ruang tiga dimensi merupakan sesuatu yang kompleks, dan koordinat semua titik pada garis tersebut biasanya direpresentasikan dengan rumus pada tiga variabel berurutan, yang digunakan untuk menyatakan himpunan selesaiannya.

Jika bidang-bidang berpotongan pada semua titik, sistem tersebut disebut tergantung secara kongruen (coincidentally dependent), lihat gambar c. Hal ini mengindikasikan bahwa persamaan-persamaan pada sistem tersebut hanya berbeda pada pengali konstannya, atau dengan kata lain persamaan-persamaan tersebut sebenarnya sama. Himpunan selesaian dari kasus ini adalah sembarang tiga bilangan berurutan (a, b, c) yang memenuhi persamaan tersebut. Dan yang terakhir, suatu SPLTV mungkin juga tidak memiliki selesaian atau himpunan selesaiannya adalah himpunan kosong. Kasus ini dapat terjadi dengan cara yang berbeda-beda, dan yang paling sering muncul adalah kasus yang ditunjukkan oleh gambar d di atas. Pada kasus yang tidak memiliki selesaian ini, suatu tiga bilangan berurutan mungkin tidak memenuhi semua persamaan, hanya memenuhi satu atau dua persamaan. Untuk lebih memahami mengenai selesaian dari SPLTV, perhatikan contoh berikut.

Contoh: Menentukan Solusi SPLTV atau Bukan

Tentukan apakah tiga bilangan berurutan (1, –2, 3) merupakan selesaian dari SPLTV berikut atau bukan.

dan,

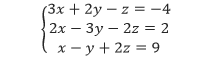
Pembahasan Substitusi 1 untuk x, –2 untuk y, dan 3 untuk z ke dalam SPLTV pertama.

Karena (1, –2, 3) tidak memenuhi salah satu persamaan pada SPLTV pertama, maka tiga bilangan berurutan tersebut bukan selesaian dari SPLTV tersebut. Selanjutnya kita gunakan substitusi yang sama pada SPLTV kedua.

Karena tiga bilangan berurutan (1, –2, 3) memenuhi ketiga persamaan pada SPLTV kedua, maka tiga bilangan berurutan tersebut merupakan solusi dari SPLTV tersebut.